Circunferencia

Circunferencia

Circunferencia

Algunos de los elementos de una circunferencia son: diámetro, radio, cuerda y arco. Para experimentar con las propiedades de la circunferencia, se ata un hilo alrededor de una lata y se mide la longitud del hilo (longitud de la circunferencia). Utilizando el hilo, se divide la tapa de la lata en dos partes iguales y se mide la longitud (diámetro de la tapa). Se divide el valor medido de la circunferencia (C) por el del diámetro (D); si se repite varias veces esta operación con distintos objetos circulares, se obtiene siempre un cociente C :D alrededor de 3:1, sean los círculos grandes o pequeños. Este cociente se representa con el símbolo p.

Circunferencia, en geometría, curva plana cerrada en la que cada uno de sus puntos equidista de un punto fijo, llamado centro de la circunferencia. No se debe confundir con el círculo (superficie), aunque ambos conceptos están estrechamente relacionados. La circunferencia pertenece a la clase de curvas conocidas como cónicas, pues una circunferencia se puede definir como la intersección de una superficie cónica con un plano perpendicular a su eje.

Cualquier segmento rectilíneo que pasa por el centro y cuyos extremos están en la circunferencia se denomina diámetro. Un radio es un segmento que va desde el centro hasta la circunferencia. Una cuerda es un segmento rectilíneo cuyos extremos son dos puntos de la circunferencia. Un arco de circunferencia es la parte de ésta que está delimitada por dos puntos. Un ángulo central es un ángulo cuyo vértice es el centro y cuyos lados son dos radios.

La proporción entre la longitud de la circunferencia y su diámetro es una constante, representada por el símbolo p, o pi. Es una de las constantes matemáticas más importantes y desempeña un papel fundamental en muchos cálculos y demostraciones en matemáticas, física y otras ciencias, así como en ingeniería. Pi es aproximadamente 3,141592, aunque considerar 3,1416, o incluso 3,14, es suficiente para la mayoría de los cálculos. El matemático griego Arquímedes encontró que el valor de p estaba entre 3 + ‡ y 3 + .

El centro de la circunferencia es centro de simetría, y cualquier diámetro es eje de simetría.

2

POSICIONES RELATIVAS DE UNA RECTA Y UNA CIRCUNFERENCIA

Una recta y una circunferencia pueden ser exteriores, si no se cortan (no tienen ningún punto en común), tangentes, si sólo se tocan en un punto (punto de tangencia), y secantes si tienen dos puntos comunes.

Una recta tangente a una circunferencia es perpendicular al radio que une el centro con el punto de tangencia.

3

POSICIONES RELATIVAS DE DOS CIRCUNFERENCIAS

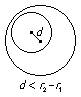
Dos circunferencias también pueden no tocarse, ser tangentes o ser secantes según tengan ninguno, uno o dos puntos comunes, respectivamente. Sin embargo, se pueden precisar más las posiciones relativas de dos circunferencias según la distancia entre sus centros, d, y las longitudes de sus radios, r₁ y r₂:

• Exteriores: si no tienen puntos comunes y la distancia entre sus centros es mayor que la suma de sus radios.

• Tangentes exteriores: si tienen un punto común y la distancia entre sus centros es igual a la suma de sus radios.

• Secantes: si tienen dos puntos comunes.

• Tangentes interiores: si tienen un punto común y la distancia entre sus centros es igual a la diferencia de sus radios.

• Interior una a la otra: si no tienen ningún punto común y la distancia entre sus centros es menor que la diferencia de sus radios.

• Concéntricas: si tienen el mismo centro.

4

CIRCUNFERENCIAS Y POLÍGONOS

La circunferencia inscrita en un polígono regular es la que tiene su centro en el del polígono y es tangente a todos sus lados. Su radio es igual a la apotema del polígono.

La circunferencia circunscrita a un polígono regular es la que pasa por todos sus vértices.

Los triángulos, aunque no sean regulares, tienen siempre circunferencia inscrita (tangente a sus tres lados) y circunscrita (que pasa por sus tres vértices). Se llama circunferencia exinscrita a un triángulo, a la que es tangente a uno de sus lados y a las prolongaciones de los otros dos.

5

ÁNGULOS EN LA CIRCUNFERENCIA

Como ya se ha dicho anteriormente, un ángulo central de una circunferencia es el que tiene su vértice en el centro de ésta. La medida de un ángulo central es igual a la del arco que abarca.

Un ángulo inscrito en una circunferencia es aquel cuyo vértice está sobre ella y cuyos lados la cortan en sendos puntos. La medida de un ángulo inscrito es la mitad de la del arco que abarca.

Un ángulo semiinscrito en una circunferencia es aquel cuyo vértice, V, está sobre ella, uno de sus lados la corta y el otro es tangente en V. La medida de un ángulo semiincrito es la mitad de la del arco que abarca.

En una circunferencia, un ángulo interior es el que tiene su vértice en el interior de la misma. Su medida es la mitad de la suma de la medida del arco que abarcan sus lados con el arco que abarcan sus prolongaciones.

Un ángulo exterior a una circunferencia es el que tiene su vértice en el exterior de la misma. Su medida es la semidiferencia de los dos arcos que abarcan sus lados sobre la circunferencia.