Gas

Gas

Gas, sustancia en uno de los tres estados diferentes de la materia ordinaria, que son el sólido, el líquido y el gaseoso. Los sólidos tienen una forma bien definida y son difíciles de comprimir. Los líquidos fluyen libremente y están limitados por superficies que forman por sí solos. Los gases se expanden libremente hasta llenar el recipiente que los contiene, y su densidad es mucho menor que la de los líquidos y sólidos.

2

LEY DE LOS GASES IDEALES

Leyes de Boyle-Mariotte y de Charles y Gay-Lussac

La ley de Boyle-Mariotte, descubierta a mediados del siglo XVII, afirma que el volumen de un gas varía inversamente con la presión si se mantiene constante la temperatura. La ley de Charles y Gay-Lussac, formulada alrededor de un siglo después, afirma que el volumen de un gas es directamente proporcional a su temperatura absoluta si la presión se mantiene constante.

La teoría atómica de la materia define los estados, o fases, de acuerdo al orden que implican. Las moléculas tienen una cierta libertad de movimientos en el espacio. Estos grados de libertad microscópicos están asociados con el concepto de orden macroscópico. Las moléculas de un sólido están colocadas en una red, y su libertad está restringida a pequeñas vibraciones en torno a los puntos de esa red. En cambio, un gas no tiene un orden espacial macroscópico. Sus moléculas se mueven aleatoriamente, y solo están limitadas por las paredes del recipiente que lo contiene.

Se han desarrollado leyes empíricas que relacionan las variables macroscópicas. En los gases ideales, estas variables incluyen la presión (p), el volumen (V) y la temperatura (T). La ley de Boyle-Mariotte afirma que el volumen de un gas a temperatura constante es inversamente proporcional a la presión. La ley de Charles y Gay-Lussac afirma que el volumen de un gas a presión constante es directamente proporcional a la temperatura absoluta. La combinación de estas dos leyes proporciona la ley de los gases ideales pV = nRT (n es el número de moles), también llamada ecuación de estado del gas ideal. La constante de la derecha, R, es una constante universal cuyo descubrimiento fue una piedra angular de la ciencia moderna.

3

TEORÍA CINÉTICA DE LOS GASES

Con la llegada de la teoría atómica de la materia, las leyes empíricas antes mencionadas obtuvieron una base microscópica. El volumen de un gas refleja simplemente la distribución de posiciones de las moléculas que lo componen. Más exactamente, la variable macroscópica V representa el espacio disponible para el movimiento de una molécula. La presión de un gas, que puede medirse con manómetros situados en las paredes del recipiente, registra el cambio medio de momento lineal que experimentan las moléculas al chocar contra las paredes y rebotar en ellas. La temperatura del gas es proporcional a la energía cinética media de las moléculas, por lo que depende del cuadrado de su velocidad. La reducción de las variables macroscópicas a variables mecánicas como la posición, velocidad, momento lineal o energía cinética de las moléculas, que pueden relacionarse a través de las leyes de la mecánica de Newton, debería de proporcionar todas las leyes empíricas de los gases. En general, esto resulta ser cierto.

La teoría física que relaciona las propiedades de los gases con la mecánica clásica se denomina teoría cinética de los gases. Además de proporcionar una base para la ecuación de estado del gas ideal, la teoría cinética también puede emplearse para predecir muchas otras propiedades de los gases, entre ellas la distribución estadística de las velocidades moleculares y las propiedades de transporte como la conductividad térmica, el coeficiente de difusión o la viscosidad.

3.1

Ecuación de Van der Waals

Johannes D. van der Waals

El físico holandés Johannes Diderik van der Waals fue galardonado con el Premio Nobel de Física en 1910. Interesado en la termodinámica, Waals desarrolló una teoría que viene expresada en la ecuación de estado que lleva su nombre.

La ecuación de estado del gas ideal no es del todo correcta: los gases reales no se comportan exactamente así. En algunos casos, la desviación puede ser muy grande. Por ejemplo, un gas ideal nunca podría convertirse en líquido o sólido por mucho que se enfriara o comprimiera. Por eso se han propuesto modificaciones de la ley de los gases ideales, pV = nRT. Una de ellas, muy conocida y particularmente útil, es la ecuación de estado de Van der Waals (p + a/v²)(v - b) = RT, donde v = V/n, y a y b son parámetros ajustables determinados a partir de medidas experimentales en gases reales. Son parámetros de la sustancia y no constantes universales, puesto que sus valores varían de un gas a otro.

La ecuación de Van der Waals también tiene una interpretación microscópica. Las moléculas interaccionan entre sí. La interacción es muy repulsiva a corta distancia, se hace ligeramente atractiva a distancias intermedias y desaparece a distancias más grandes. La ley de los gases ideales debe corregirse para considerar las fuerzas atractivas y repulsivas. Por ejemplo, la repulsión mutua entre moléculas tiene el efecto de excluir a las moléculas vecinas de una cierta zona alrededor de cada molécula. Así, una parte del espacio total deja de estar disponible para las moléculas en su movimiento aleatorio. En la ecuación de estado, se hace necesario restar este volumen de exclusión (b) del volumen del recipiente; de ahí el término (v - b).

3.2

Transiciones de fase

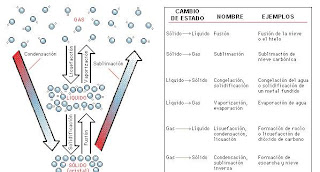
Cambios de estado

La materia existe en diferentes fases o estados. Modificando la temperatura y la presión de una muestra de materia, ésta puede pasar de uno de sus estados (sólido, líquido o gaseoso) a otro; se trata de una transición de fase o cambio de estado.

A temperaturas bajas (a las que el movimiento molecular se hace menor) y presiones altas o volúmenes reducidos (que disminuyen el espacio entre las moléculas), las moléculas de un gas pasan a ser influidas por la fuerza de atracción de las otras moléculas. Bajo determinadas condiciones críticas, todo el sistema entra en un estado ligado de alta densidad y adquiere una superficie límite. Esto implica la entrada en el estado líquido. El proceso se conoce como transición de fase o cambio de estado. La ecuación de Van der Waals permite estas transiciones de fase, y también describe una región de coexistencia entre ambas fases que termina en un punto crítico, por encima del cual no existen diferencias físicas entre los estados gaseoso y líquido. Estos fenómenos coinciden con las observaciones experimentales. En la práctica se emplean ecuaciones más complejas que la ecuación de Van der Waals.

La mejor comprensión de las propiedades de los gases a lo largo del último siglo ha llevado a la explotación a gran escala de los principios de la física, química e ingeniería en aplicaciones industriales y de consumo.

Ley de Avogadro

Ley de Avogadro

Amedeo Avogadro

Nacido en Italia, el físico y químico Amedeo Avogadro destacó por sus trabajos sobre gases. En 1811 formuló la ley que hoy lleva su nombre, y que tardó casi 40 años en ser aceptada de forma universal.

Ley de Avogadro, ley fundamental en química que establece que bajo idénticas condiciones de temperatura y presión, volúmenes iguales de gases contienen el mismo número de moléculas. Esta ley fue enunciada por primera vez como hipótesis por el físico italiano Amedeo Avogadro en 1811. Los químicos y físicos italianos continuaron desarrollando esta hipótesis, y en la década de 1850, gracias a los esfuerzos del químico italiano Stanislao Cannizzaro, la ley de Avogadro llegó a aceptarse universalmente.

Circuito eléctrico

Circuito eléctrico

Elementos de un circuito eléctrico

Símbolos de algunos elementos de un circuito eléctrico.

Circuito eléctrico, trayecto o ruta de una corriente eléctrica. El término se utiliza principalmente para definir un trayecto continuo compuesto por conductores y dispositivos conductores, que incluye una fuente de fuerza electromotriz que transporta la corriente por el circuito. Un circuito de este tipo se denomina circuito cerrado, y aquéllos en los que el trayecto no es continuo se denominan abiertos. Un cortocircuito es un circuito en el que se efectúa una conexión directa, sin resistencia, inductancia ni capacitancia apreciables, entre los terminales de la fuente de fuerza electromotriz.

2

LEY DE OHM

Circuitos eléctricos

La manera más simple de conectar componentes eléctricos es disponerlos de forma lineal, uno detrás del otro. Este tipo de circuito se denomina “circuito en serie”, como el que aparece a la izquierda de la ilustración. Si una de las bombillas del circuito deja de funcionar, la otra también lo hará debido a que se interrumpe el paso de corriente por el circuito. Otra manera de conectarlo sería que cada bombilla tuviera su propio suministro eléctrico, de forma totalmente independiente, y así, si una de ellas se funde, la otra puede continuar funcionando. Este circuito se denomina “circuito en paralelo”, y se muestra a la derecha de la ilustración.

La corriente fluye por un circuito eléctrico siguiendo varias leyes definidas. La ley básica del flujo de la corriente es la ley de Ohm, así llamada en honor a su descubridor, el físico alemán Georg Ohm. Según la ley de Ohm, la cantidad de corriente que fluye por un circuito formado por resistencias puras es directamente proporcional a la fuerza electromotriz aplicada al circuito, e inversamente proporcional a la resistencia total del circuito. Esta ley suele expresarse mediante la fórmula I = V/R, siendo I la intensidad de corriente en amperios, V la fuerza electromotriz en voltios y R la resistencia en ohmios. La ley de Ohm se aplica a todos los circuitos eléctricos, tanto a los de corriente continua (CC) como a los de corriente alterna (CA), aunque para el análisis de circuitos complejos y circuitos de CA deben emplearse principios adicionales que incluyen inductancias y capacitancias.

Un circuito en serie es aquél en que los dispositivos o elementos del circuito están dispuestos de tal manera que la totalidad de la corriente pasa a través de cada elemento sin división ni derivación en circuitos paralelos.

Cuando en un circuito hay dos o más resistencias en serie, la resistencia total se calcula sumando los valores de dichas resistencias. Si las resistencias están en paralelo, el valor total de la resistencia del circuito se obtiene mediante la fórmula

En un circuito en paralelo los dispositivos eléctricos, por ejemplo las lámparas incandescentes o las celdas de una batería, están dispuestos de manera que todos los polos, electrodos y terminales positivos (+) se unen en un único conductor, y todos los negativos (-) en otro, de forma que cada unidad se encuentra, en realidad, en una derivación paralela. El valor de dos resistencias iguales en paralelo es igual a la mitad del valor de las resistencias componentes y, en cada caso, el valor de las resistencias en paralelo es menor que el valor de la más pequeña de cada una de las resistencias implicadas. En los circuitos de CA, o circuitos de corrientes variables, deben considerarse otros componentes del circuito además de la resistencia.

3

LEYES DE KIRCHHOFF

Leyes de Kirchhoff

En este circuito eléctrico formado por dos generadores, de fuerzas electromotrices e 1 y e 2, y tres resistencias, R 1, R 2 y R 3, se puede aplicar la ley de los nudos al nudo B y la ley de las mallas a las redes ABEF y BCDE.

Si un circuito tiene un número de derivaciones interconectadas, es necesario aplicar otras dos leyes para obtener el flujo de corriente que recorre las distintas derivaciones. Estas leyes, descubiertas por el físico alemán Gustav Robert Kirchhoff, son conocidas como las leyes de Kirchhoff. La primera, la ley de los nudos, enuncia que en cualquier unión en un circuito a través del cual fluye una corriente constante, la suma de las intensidades que llegan a un nudo es igual a la suma de las intensidades que salen del mismo. La segunda ley, la ley de las mallas afirma que, comenzando por cualquier punto de una red y siguiendo cualquier trayecto cerrado de vuelta al punto inicial, la suma neta de las fuerzas electromotrices halladas será igual a la suma neta de los productos de las resistencias halladas y de las intensidades que fluyen a través de ellas. Esta segunda ley es sencillamente una ampliación de la ley de Ohm.

4

IMPEDANCIA

La aplicación de la ley de Ohm a los circuitos en los que existe una corriente alterna se complica por el hecho de que siempre estarán presentes la capacitancia y la inductancia. La inductancia hace que el valor máximo de una corriente alterna sea menor que el valor máximo de la tensión; la capacitancia hace que el valor máximo de la tensión sea menor que el valor máximo de la corriente. La capacitancia y la inductancia inhiben el flujo de corriente alterna y deben tomarse en cuenta al calcularlo. La intensidad de corriente en los circuitos de CA puede determinarse gráficamente mediante vectores o con la ecuación algebraica

en la que L es la inductancia, C la capacitancia y f la frecuencia de la corriente. El valor obtenido en el denominador de la fracción se denomina impedancia del circuito y suele representarse por la letra Z. Por consiguiente, la ley de Ohm para los circuitos integrados suele expresarse por la ecuación sencilla I = e / Z.

Espectrómetro de masas

Espectrómetro de masas

Francis William Aston

El físico británico Francis William Aston fue galardonado con el Premio Nobel de Química en 1922. Aston construyó, en 1919, el primer espectrómetro de masas, con el que demostró que muchos elementos están formados por dos o más isótopos.

Espectrómetro de masas, aparato que convierte moléculas en iones, y que separa estos iones en función de su proporción de masa y carga. Los espectrómetros de masas se utilizan para identificar átomos e isótopos, y determinar la composición química de una muestra.

Espectrómetro de masas

En un espectrómetro de masas se ioniza una muestra de gas mediante un haz de electrones y se aceleran los iones hacia un imán, que los separa según su masa (arriba a la derecha). Los iones con una masa determinada llegan al detector, que suele estar conectado a un ordenador o computadora que procesa los datos (abajo).

Si bien hoy día se utilizan varios tipos de espectrómetros de masas, todos ellos están relacionados con el dispositivo desarrollado en 1919 por el físico británico Francis William Aston. El instrumento de Aston usaba un haz fino de iones con carga positiva, que se desviaba en primer lugar mediante un campo eléctrico y que a continuación se desviaba en la dirección opuesta con un campo magnético. La cantidad de partículas resultantes de la deflexión se registraba en una placa fotográfica, y dependía de su masa y velocidad. Cuanto mayor era la masa del ion, menor era su deflexión. Aston midió las masas moleculares de los isótopos de muchos elementos, y comprobó la abundancia relativa de éstos en la naturaleza.

Todos los espectrómetros de masas cuentan con cuatro características comunes: (1) un sistema para introducir la sustancia que se desea analizar en el instrumento, (2) un sistema para ionizar la sustancia, (3) un acelerador que dirige los iones hacia el instrumento de medida y (4) un sistema para separar los distintos iones analizados y para registrar el espectro de masas de la sustancia.

2

EL ESPECTRÓMETRO DE MASAS DE DEFLEXIÓN MAGNÉTICA

Este tipo de espectrómetro de masas crea iones con carga positiva a partir de una muestra y acelera los iones utilizando un campo electrostático. Un campo magnético desvía los iones en función de su masa, y chocan contra el detector aquéllos que tienen una masa determinada. Los iones de menor masa se desvían demasiado y no alcanzan el detector, mientras que los iones más pesados no se desvían lo suficiente. La intensidad del campo magnético varía lentamente, para que el detector pueda medir las proporciones relativas de todos los componentes de la muestra. El detector suele estar conectado a un ordenador que procesa toda esta información.

3

APLICACIONES DE LOS ESPECTRÓMETROS

Los espectrómetros de masas pueden proporcionar un alto grado de resolución como ayuda a los análisis de mezclas complejas. Por ejemplo, los productos del refinado y procesamiento del petróleo, que contienen normalmente hidrocarburos muy similares, son difíciles de separar con métodos de análisis químico convencionales, pero pueden ser aislados y analizados con un espectrómetro de masas. Se consigue una mayor precisión con espectrómetros de masas en serie, que consisten en varios espectrómetros colocados uno tras otro. En el campo de la biología molecular, los espectrómetros en serie (con dos espectrómetros de masas) permiten determinar en pocos minutos la secuencia lineal de los aminoácidos de una proteína. Estos espectrómetros de masas son más de mil veces más precisos que un dispositivo único, lo que hace que resulten muy útiles para analizar cantidades muy pequeñas de compuestos biológicos con masas moleculares muy altas. Los dispositivos más sensibles que pueden emplearse en la espectrometría de masas son los aceleradores electrostáticos en serie, que comprenden varios espectrómetros de masas dispuestos en serie y conectados a un potente acelerador electrostático de partículas.

Último teorema de Fermat

Último teorema de Fermat

Último teorema de Fermat, en matemáticas, famoso teorema origen de importantes descubrimientos en el álgebra y el análisis. Al estudiar Las aritméticas, obra del matemático griego Diofante, el matemático francés Pierre de Fermat se interesó por el capítulo sobre los números pitagóricos —esto es, los conjuntos de tres números naturales, a, b y c, como 3, 4 y 5, para los que se cumple la ecuación a² + b² = c². Fermat propuso que si se altera el teorema de Pitágoras de manera que sea aⁿ + bⁿ = cⁿ, esta ecuación no tiene solución para números naturales (excluido el cero) si n es un número natural mayor que 2. Por ejemplo, no se puede encontrar un conjunto de números naturales a, b y c (distintos de cero) que cumplan a³ + b³ = c³. Fermat escribió en su ejemplar de Las aritméticas: “He descubierto una demostración realmente extraordinaria de esto, que no cabe aquí por ser este margen demasiado pequeño”.

Muchos matemáticos trataron de demostrar esta afirmación de Fermat o de encontrar una excepción para demostrar que era falsa. En 1908 se estableció un premio de 100.000 marcos, administrado por la Universidad de Gotinga en Alemania, para quien fuera capaz de encontrar una demostración (aunque no por una excepción) que pudiera verificarse antes del 13 de septiembre del 2007. El teorema fue comprobado para grandes exponentes utilizando computadoras. En junio de 1993, Andrew Wiles, un matemático británico de la Universidad de Princeton, afirmó que había logrado demostrar el teorema. En diciembre del mismo año, los expertos encontraron un fallo en la demostración, pero Wiles siguió trabajando en ella hasta conseguir resolver el fallo dos años más tarde.

Teorema de Pitágoras

Teorema de Pitágoras

Teorema de Pitágoras, teorema que relaciona los tres lados de un triángulo rectángulo, y que establece que el cuadrado del lado mayor (hipotenusa) es igual a la suma de los cuadrados de los otros dos lados (catetos).

El teorema de Pitágoras permite calcular uno de los lados de un triángulo rectángulo si se conocen los otros dos. Así, permite calcular la hipotenusa a partir de los dos catetos:

o bien, calcular un cateto conocidos la hipotenusa y el otro cateto:

Demostración matemática

Demostración matemática

Demostración matemática: figuras 1 y 2

Estos diagramas se pueden utilizar para demostrar el teorema de Pitágoras, que dice que si un triángulo rectángulo tiene catetos A y B e hipotenusa C, entonces A2 + B2 = C2. Las figuras 1 y 2 contienen ambas cuatro triángulos rectángulos con catetos A y B e hipotenusa C. Dado que ambas figuras tienen la misma área, si se eliminan los cuatro triángulos de la figura 1, el área restante debe ser igual a la que queda si se eliminan de la figura 2. En la figura 1, el área restante es A2 + B2, y en la figura 2, es C2. Por tanto, A2 + B2 = C2, lo que demuestra el teorema de Pitágoras.

Demostración matemática, argumento utilizado para mostrar la veracidad de una proposición matemática. En las matemáticas modernas una demostración comienza con una o más declaraciones denominadas premisas, y prueba, utilizando las reglas de la lógica, que si las premisas son verdaderas, entonces una determinada conclusión debe ser también cierta.

Los métodos y estrategias utilizados para construir un argumento matemático convincente han evolucionado desde los tiempos antiguos y todavía siguen cambiando. Esto se puede comprobar con el teorema de Pitágoras, que recibe su nombre del matemático y filósofo griego del siglo V a.C. Pitágoras, y que establece que en un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. La mayor parte de las civilizaciones antiguas consideraron que este teorema era cierto pues coincidía con sus observaciones experimentales. Sin embargo, los griegos, entre otros, comprobaron que la simple observación o la opinión común no garantizan la verdad matemática. Así, antes del siglo V a.C. se aceptaba que todas las longitudes se podían expresar como el cociente de dos números enteros, pero un anónimo matemático griego demostró que esto no era posible con la longitud de la diagonal de un cuadrado de área unidad.

Un ejemplo de demostración matemática es el siguiente razonamiento que prueba que el teorema de Pitágoras es cierto. Las figuras 1 y 2 muestran que la relación A²+ B² = C² se cumple para cualquier triángulo rectángulo con catetos A y B e hipotenusa C. La figura 1 muestra cómo un cuadrado de lado A + B se puede dividir en cuatro triángulos rectángulos, un cuadrado de lado A y un cuadrado de lado B. La figura 2 muestra que el mismo cuadrado de lado A + B se puede también dividir en cuatro triángulos rectángulos más un cuadrado de lado C. Como los dos cuadrados de lado A + B deben tener igual área, seguirán teniendo la misma superficie si se eliminan los cuatro triángulos rectángulos en ambos. El área total restante en el lado izquierdo es A² +  B², y el área del cuadrado que queda en el lado derecho es C². Por tanto, A² + B² = C².

El matemático griego Euclides estableció algunas de las consideraciones fundamentales de las demostraciones matemáticas modernas. En su libro Elementos, escrito hacia el año 300 a.C., se encuentran bastantes demostraciones en los campos de la geometría y del álgebra. El libro ilustra el sistema griego de escribir demostraciones matemáticas empezando por identificar claramente los supuestos iniciales y a partir de éstos razonar de una manera lógica hasta obtener la conclusión deseada. Además, en este tipo de argumentos Euclides utilizaba resultados de otras demostraciones cuya certeza era conocida, llamados teoremas, y proposiciones aceptadas explícitamente por ser evidentes, llamadas axiomas. Este sistema aún se utiliza hoy.

En el siglo XX se han escrito demostraciones tan complejas que una sola persona no es capaz de entender todos y cada uno de los razonamientos utilizados. En el año 1976 se utilizó un ordenador o computadora para completar la demostración del teorema de los cuatro colores. Este teorema dice que cuatro colores son suficientes para colorear cualquier mapa cumpliendo que dos regiones con una línea fronteriza común tienen distintos colores. El uso de un ordenador en esta demostración produjo discusiones considerables en la comunidad matemática. El principal problema es saber si el teorema se puede considerar demostrado sin que ningún ser humano compruebe todos los pasos y detalles de la demostración.

Teorema de Bernoulli

Teorema de Bernoulli

Pelota con efecto

Cuando una pelota se tira con efecto, su trayectoria se curva debido a las fuerzas que surgen al girar sobre sí misma. La superficie rugosa arrastra el aire adyacente y lo hace girar. Esto crea una zona de alta presión en un lado y de baja presión en el otro; la diferencia de presiones hace que su trayectoria se curve.

Teorema de Bernoulli, principio físico que implica la disminución de la presión de un fluido (líquido o gas) en movimiento cuando aumenta su velocidad. Fue formulado en 1738 por el matemático y físico suizo Daniel Bernoulli, y anteriormente por Leonhard Euler. El teorema afirma que la energía total de un sistema de fluidos con flujo uniforme permanece constante a lo largo de la trayectoria de flujo. Puede demostrarse que, como consecuencia de ello, el aumento de velocidad del fluido debe verse compensado por una disminución de su presión.

El teorema se aplica al flujo sobre superficies, como las alas de un avión o las hélices de un barco. Las alas están diseñadas para que obliguen al aire a fluir con mayor velocidad sobre la superficie superior que sobre la inferior, por lo que la presión sobre esta última es mayor que sobre la superior. Esta diferencia de presión proporciona la fuerza de sustentación que mantiene al avión en vuelo. Una hélice también es un plano aerodinámico, es decir, tiene forma de ala. En este caso, la diferencia de presión que se produce al girar la hélice proporciona el empuje que impulsa al barco. El teorema de Bernoulli también se emplea en las toberas, donde se acelera el flujo reduciendo el diámetro del tubo, con la consiguiente caída de presión. Asimismo se aplica en los caudalímetros de orificio, también llamados venturi, que miden la diferencia de presión entre el fluido a baja velocidad que pasa por un tubo de entrada y el fluido a alta velocidad que pasa por un orificio de menor diámetro, con lo que se determina la velocidad de flujo y, por tanto, el caudal.