La circunferencia y el círculo
El aro de una canasta de baloncesto y un anillo son circunferencias. La circunferencia es una figura curva, cerrada (no tiene un punto de principio ni de final) y plana (la dibujamos sobre una superficie plana), cuyos puntos están todos a la misma distancia de su centro. Si colocamos el anillo, por ejemplo, sobre una lámina de papel y coloreamos la zona que queda dentro de la circunferencia, esta superficie plana coloreada es un círculo.
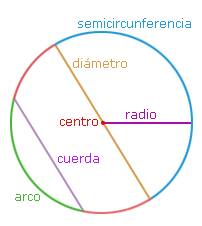
ELEMENTOS DE LA CIRCUNFERENCIA
Algunos elementos de la circunferencia son: radio, cuerda, diámetro y arco.
· El radio es el segmento que une cualquier punto de la circunferencia con su centro.
· Una cuerda es un segmento que une dos puntos de la circunferencia. A la cuerda que pasa por el centro se le llama diámetro.
· El diámetro mide el doble que el radio, y divide a la circunferencia en dos semicircunferencias.
· Un arco es la parte de circunferencia comprendida entre dos de sus puntos.
| |
LONGITUD DE LA CIRCUNFERENCIA
La longitud de una circunferencia es igual a su diámetro multiplicado por el número p (que vale 3,14 y se lee “pi”): Longitud de la circunferencia = diámetro × p
Si quisiéramos, por ejemplo, saber lo que avanza la rueda de una bicicleta de 40 cm de diámetro cada vez que da una vuelta, hallaríamos la longitud de su circunferencia: Longitud = 40 × 3,14 = 125,6 cm
Si quieres, puedes practicar con el ejemplo siguiente.
Si en cada viaje, un tiovivo da 30 vueltas, ¿qué distancia recorrerás si te montas en un caballito que está a 2 metros de su eje o centro?
Cada vuelta recorrerás una circunferencia de 2 m de radio; por tanto, su diámetro será: diámetro = 2 × radio = 4 m
Y la longitud de la circunferencia: longitud = diámetro × 3,14 longitud = 4 × 3,14 = 12,56 m
Si en cada viaje se dan 30 vueltas, la distancia recorrida será: 30 × 12,56 = 376,8 m
POSICIONES DE UNA RECTA Y UNA CIRCUNFERENCIA
Sobre una superficie plana, una recta y una circunferencia pueden estar en una de estas tres posiciones:
1. La recta exterior a la circunferencia: no tienen ningún punto en común.
| |
2. La recta tangente a la circunferencia: tienen un punto en común.
| |
3. La recta secante a la circunferencia: tienen dos puntos en común.
| |
POSICIONES DE DOS CIRCUNFERENCIAS
Dos circunferencias sobre una superficie plana, pueden ocupar distintas posiciones una respecto a la otra, pudiendo ser: exteriores, interiores, concéntricas, tangentes exteriores, tangentes interiores o secantes.
1. Exteriores: no tienen ningún punto en común.
| |
2. Interiores: no tienen ningún punto en común.
| |
3. Concéntricas: tienen el mismo centro, pero diferentes radios.
| |
4. Tangentes exteriores: tienen un punto en común.
| |
5. Tangentes interiores: tienen un punto en común.
| |
6. Secantes: tienen dos puntos en común.
| |
EL CÍRCULO
El círculo es la figura que forman una circunferencia y su interior. No debes confundir la circunferencia, que es una línea curva, con el círculo, que es la superficie que encierra esa línea.
Un sector circular es la parte de círculo comprendida entre dos radios y el arco que abarcan.
| |
Un semicírculo es la superficie limitada por un diámetro y la semicircunferencia: es la mitad del círculo.
| |
Un segmento circular es la parte de círculo comprendida entre una cuerda y su arco.
| |
ÁREA DEL CÍRCULO
El área de un círculo de radio R es igual a p por su radio al cuadrado: Área del círculo = p × R2
Vamos a calcular el área del círculo en los dos ejemplos siguientes.
1. Halla el área de una pizza que mide 15 cm de radio.
La pizza tiene forma circular, así que: Área de la pizza = p × R2
Como R2 = 152 = 225: Área = 3,14 × 225 = 706,5 cm2
2. Una diana de dardos tiene 40 cm de diámetro. Calcula el área que ocupa.
Como el diámetro es el doble del radio: Radio = diámetro : 2 Radio = 40 : 2 = 20 cm
Y como R2 = 202 = 400: Área = 3,14 × 400 = 1.256 cm2
LA CORONA CIRCULAR
Una corona circular es la zona que queda comprendida entre dos circunferencias de diferentes radios.
| |
Para hallar el área de una corona circular, restamos del área del círculo grande el área del círculo pequeño. Siendo R el radio del círculo grande y r el del pequeño,
| |
El área será: Área = p × R2 – p × r2
Si quieres, puedes practicar con el siguiente ejemplo:
Una tarta redonda se ha adornado, en su parte central, de 9 cm de radio, con mermelada de fresa, y en la corona circular que queda hasta el borde, de radio 13 cm, con nata. Halla la superficie de tarta adornada con nata.
Hallamos el área de toda la tarta (del círculo grande); como R2 = 132 = 169: Área = p × R2 = 3,14 × 169 = 530,66 cm2
Y ahora hallamos el área de la parte central(del círculo más pequeño); como r2 = 92 = 81: área = p × r2 = 3,14 × 81 = 254,34 cm2
El área de la zona adornada con nata será: Área de la corona = 530,66 – 254,34 = 276,32 cm2























No hay comentarios:
Publicar un comentario